Die statistische Normalverteilung von Aktienrenditen

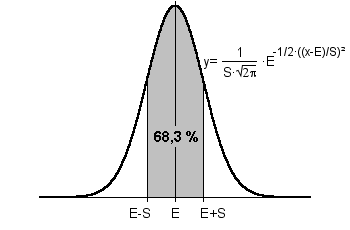
Aktienkurse besitzen kein klar definiertes Verhalten, ihre Entwicklung ist zufällig und deshalb nicht exakt berechenbar.
Mit Hilfe der Statistik bzw. Wahrscheinlichkeitsrechnung ist es jedoch trotzdem möglich, mathematisch belegte Prognosen ableiten.

Obwohl Aktienkurse zufällig sind, unterliegen sie Regeln. Ausgangspunkt der Überlegungen ist die Beobachtung, dass bestimmte Kursveränderungen immer mit einer bestimmten Häufigkeit auftreten. Mathematisch und damit praktisch fassbar wird dieser Sachverhalt durch das Modell von sog. Verteilungsdichtefunktionen.

Eine Verteilungsdichtefunktion macht Aussagen über die Häufigkeit, mit der Kursveränderungen aufgetreten sind und auftreten werden. Jeder Aktienkurs besitzt spezifische Wahrscheinlichkeiten und damit eine eigene Verteilungsdichtefunktion.

Eine Spezialform von Verteilungsdichtefunktionen sind sog. Normalverteilungen, welche eine Vielzahl von zufälligen Ereignissen in Natur und Gesellschaft beschreiben. Diese Verteilungen sind also "normal". Nach dem bedeutenem deutschen Mathematiker Johann Carl Friedrich Gauß (*1777-†1855), der ihre Bedeutung erkannte, werden sie auch als Gauß-Verteilungen bezeichnet.

Grafik: Gauß- oder Normalverteilung

Auch Aktienkurse lassen sich mit einem solchen Normalverteilungs-Modell beschreiben. Dieses Modell ist durch die besondere, glockenförmige Form der Funktion definiert. Die Fläche unter der Kurve ist auch hier ein Maß für die Wahrscheinlichkeit, mit der Daten des entsprechenden Bereichs auftreten.

Der Scheitelpunkt der Funktion liegt beim sog. Erwartungswert E. Kursveränderungen nahe diesem Wert kommen am häufigsten vor, sie besitzen also die größte Auftretenswahrscheinlichkeit. Der zweite charakteristische Parameter einer Normalverteilung ist die sog. Standartabweichung S. Dieser Parameter bestimmt die Breite der Kurve und gibt den Bereich um E an, welcher rund 2/3 aller Daten umfaßt.

Die Parameter E und S werden auch als Rendite und Volatilität (bzw. Schwankungsbreite) eines Aktienkurses bezeichnet. Beide Werte geben Aufschluss darüber, in welchem Bereich der Kurs in der Zukunft mit hoher Wahrscheinlichkeit notieren wird und liefern so Anhaltspunkte für Kursziel und Stop-Loss. Last, but not least, ist es mit dem statistischen Normalverteilungs-Modell möglich, das Chance-Risiko-Verhältnis einer Aktie bzw. eines Aktienkurses zu bestimmen, das ein wichtiges Kriterium zur Aktienauswahl darstellt.